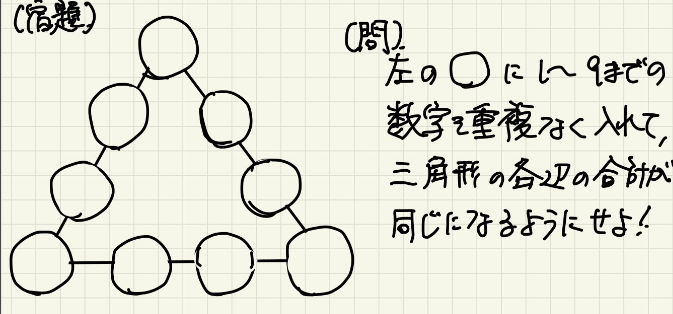
SNSに流れてきた小学生からの挑戦状に勝手に挑戦してみました！（笑）

日進市で、主に日進西中学校の生徒を中心に、生徒みずから主体性を持って学び、自分のペースで勉強できる、ICTを活用した自立学習による学びの場を提供している、セルモ日進西小学校前教室　塾長の西尾です。

SNSに流れてきた面白い問題を見つけました。

SNSに流れてきた小学生からの挑戦状に勝手に挑戦してみました！（笑）

というもので、私も勝手にこの小３からの挑戦状（宿題）に挑戦してみることにしました。

まず、１～９までの数字の合計が45

各辺の数字の合計が等しくなるのだから、各辺の合計を全部足すと当然３の倍数になる。

しかもこのとき、頂点の数字は2回足されることになるので、頂点の数字をP,Q,Rとすると、P+Q+Rも必ず3の倍数になる。

１～９の数字を1つづ使って3つの数字の組み合わせを作るとその総数は、9C3で84通り

その中でその数字の和が3の倍数になるものは、30通りもある。

さらに、その数字の組み合わせを頂点においたとき、のこりの6個の数字を2つづつペアで入れる入れ方は90通りもあるので、愚直に全部の組み合わせを調べると30✕90＝2700通りにもなる。

そこで、30通りの頂点の組み合わせが、解を持つかどうか、判定するためにExcelをうまく使って、途中の計算をすべてExcelにまかせることにしたら、わりとサクサクと解を持つかどうかの判定ができるようになった。

結果、頂点の3つの数字が以下の9通りの組み合わせのときだけ解を持つことがわかりました。

（1.2.3）（1.5.9）（4.5.6）（2.3.7）（3.7.8）（7.8.9）（1.4.7）（2.5.8）（3.6.9）

いや～久々に頭を使って、楽しかったです！

ちょうど高校生が、場合の数の復習をしていたので、いいトレーニングになりました！