今日の愛知の公立入試、数学の詳しい解説はこちらへ！
日進市で、主に日進西中学校の生徒を中心に、生徒みずから主体性を持って学び、自分のペースで勉強できる、ICTを活用した自立学習による学びの場を提供している、セルモ日進西小学校前教室 塾長の西尾です。
本日無事、令和5年の愛知県の公立高校一般入試の学力検査が終了しました。
目次
令和5年 愛知県公立高校入試 一般入試の学力検査が終了！ 数学の詳しい解説はこちらへ！
友人で、名学館小牧新町校の吉澤塾長が、個人で愛知県から入試当日の各教科の終了直後に問題、解答を入手し、即ブログにアップしてくれました！
今年も、吉澤塾長からの依頼もあって、数学の分析と解説を寄稿してみました。
数学の分析と解説
大問１
大問１は、昨年と同じく１０問。
計算問題５問と、関数、確率、整数、平面図形の小問５問の組み合わせとなっている。
難易度は、例年より、やや易しくなった感がある。
ただ、(10)の平面図形の性質は、図がなく言葉だけであらわされている問題を理解するのが難しかったと思われる。
大問１の(10)がわからなかった生徒は、数学の教科書P175をみて確認してみましょう。
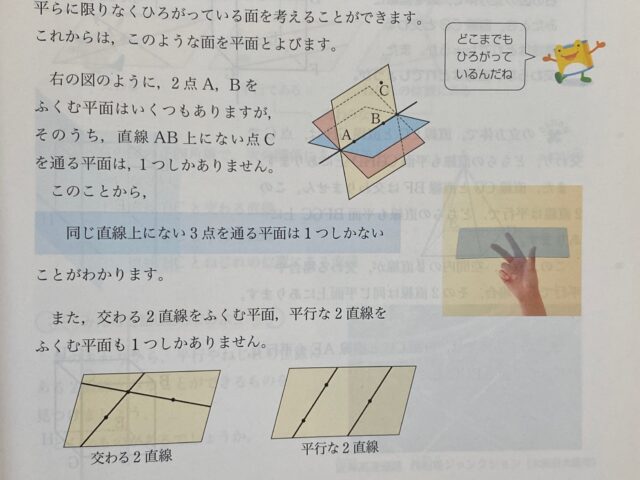
10問ある基本の１点問題で、いかにミスを少なくできたかが勝負の分かれ目かも。
大問２
（１）は統計の箱ひげ図の問題。（２点問題、ただし部分点あり）
昨年より高校から中学に落ちてきた単元で、今年始めて入試でも取り上げられた。
箱ひげ図から、四分位範囲、中央値を正しく読めていれば、（イ）（ウ）が選べるので、残りの選択肢に惑わされずに済んだはず。
（２）三角形の合同の証明問題。（２点問題、ただし部分点あり）
二等辺三角形の底角が等しいこと、平行線の錯覚が等しいことを使うのが問題から読めるので、その記号を選べば良い。
２点問題の証明としては、簡単なので、ここはしっかり取りたいところ。
（３）点P、Qが動く動点の問題。（①が１点、②が２点）
①点Pが毎秒１センチ動くこと、頂点Aから出発して、頂点Dで折り返すことに注意してx=6（6秒後）ｙの値（頂点Aからの距離）を求める。
②点Qが毎秒２センチ動くこと、頂点Cから出発して、頂点Bで折り返すことに注意して、問題用紙にあるグラフ用紙を利用し、Pの動き（青線）Qの動き（赤線）を書くことで、グラフが重なる点（頂点Aからの距離が等しい点、つまり線ABと平行になる点）を数えることで求まる。
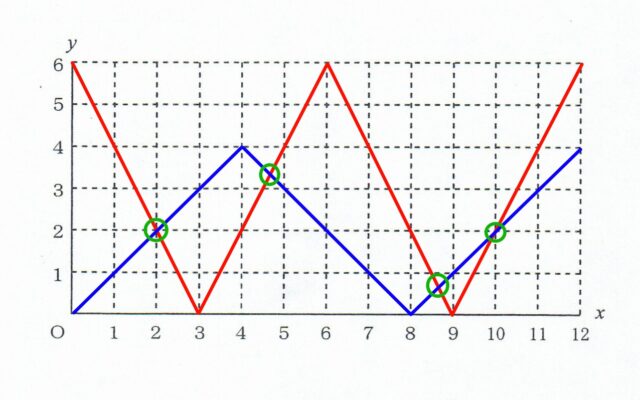
３問ある２点問題が比較的難易度が低かったし、部分点もあるので、ここでどれだけ得点できたかどうか。
大問３
図形問題
（１）
求角。
OCに補助線を引いて、OB=OC（半径なので二等辺三角形）を作れたか。また、AO//BCから、48°が二等辺三角形の底角になることに気づけたか。
二等辺三角形△OBCの頂角が42°になるので、弧ACの中心角＝48+84＝132° 角ADCは弧ACの円周角なので、132÷2＝66°
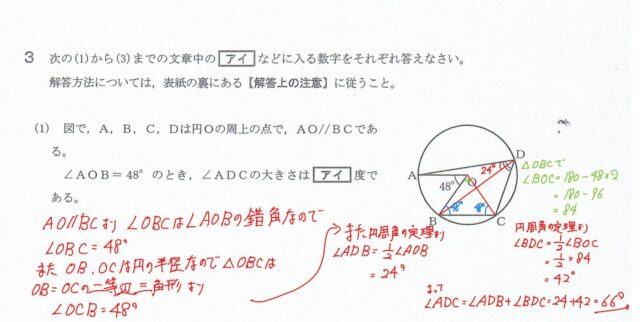
（２）
①FE//DBより△AEF∽△ABD よって、AF:AD＝1：2 よってAF=5
三平方の定理より、EF=√34
②辺BCとEDを伸ばした線が交わる点をIとする、下図より△HDF：△HBC=1：2、△GDF：△GIC=1：4、FG:GH:HC＝3：2：10
△FDCの面積は15
頂点Dを共有しているので、底辺の比＝面積の比となり、△DGHの面積は、15✕2/15＝2
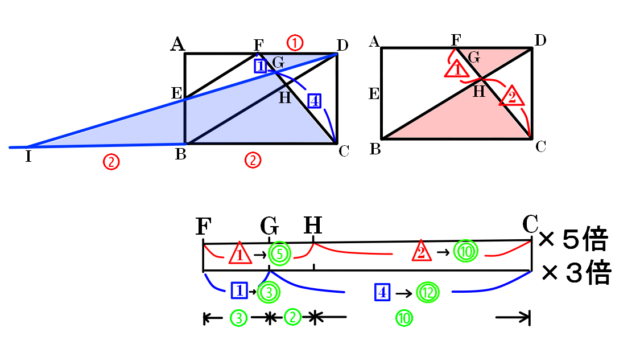
（３）
①底面となる台形は、CB=DA=５なので左右対称の形となる。左右が3：4：5の直角三角形になることから高さは4
面積は、（3＋9）✕4✕1/2＝24
②求める立体を左右の三角錐と、中央の三角柱（四角柱の半分）に分け計算する
中央の三角柱は 四角柱の体積（3✕4☓7＝84）の半分なので42
左右の三角錐は、3☓4✕1/2✕7✕1/3＝14
求める立体の体積は42＋14✕２＝70
全体を通して、大問２全体が2点問題としては易化しており、さらに大問３も易化した影響から平均1３～14点前後まで上がると予想。
実際、既に推薦を決めた生徒に解いてもらったところ、21点、19点、15点と、3人とも過去問よりも、3～4点高い得点でした。
公立高校入試としては、得点が取りやすく差がつきにくい問題になったと思われます。
無料体験授業で、試してみませんか？
お子さんの主体性を育みながら、高い学力が身につくセルモのパソコン個別学習を無料で体験していただくことができます。
- パソコン学習ってどんなの？
- パソコン学習を、ウチの子はやりたがるかしら？
- パソコン学習の効果は？
どうぞ、体験授業でお確かめください。
当学習塾へのアクセス（日進市浅田町）
住所：日進市浅田町東田面101 2A（日進西小学校の目の前です）お申し込み・お問い合わせは、LINE・お電話・ネットから
LINEからも、お申し込み・お問い合わせができます
