今日の愛知の公立入試が無事終了、数学の詳しい解説はこちらへ!

日進市で、主に日進西中学校の生徒を中心に、生徒みずから主体性を持って学び、自分のペースで勉強できる、ICTを活用した自立学習による学びの場を提供している、セルモ日進西小学校前教室 塾長の西尾です。
本日無事、令和6年の愛知県の公立高校一般入試の学力検査が終了しました。
令和6年 愛知県公立高校入試 一般入試の学力検査が終了! 数学の詳しい解説はこちらへ!

友人で、名学館小牧新町校の吉澤塾長が、個人で愛知県から入試当日の各教科の終了直後に問題、解答を入手し、即ブログにアップしてくれました!
今年も、吉澤塾長からの依頼もあって、数学の分析と解説を寄稿してみました。

いや~昨年はとっても簡単で楽勝だったのに、今年は打って変わって一気に難しくなりました。
大問3は、辺の長さを求めるのに、相似比の計算を2回やらないと解けなかったり、直角三角形の辺の比を三平方の定理で出した後、辺の長さに変換したりといった、これまでになかった手順、解法を求められてきました。
昨年が簡単過ぎたから今年はかなり難化するとは予想していたものの、ここまで上がるとは正直おどろきでしたね。
数学の分析と解説
大問1
大問1は、昨年と同じく10問。
計算問題5問と、不等式、関数、平方根、箱ひげ図、平面図形の小問5問の組み合わせとなっている。
難易度は、例年より、難しくなった感がある。
(9)の箱ひげ図は、ヒストグラムのグラフをみて、そこから箱ひげ図がどうなるかを考える問題です。
ヒストグラムのグラフから、最小値、最大値、中央値、第1,第3四分位数を特定出来たかどうか?
10問ある基本の1点問題で、いかにミスを少なくできたかが勝負の分かれ目かも。
大問2
(1)場合の数を考える問題(配点2点)
落ち着いてすべての事象を樹形図などで書き出し、丁寧に数えることが大切。
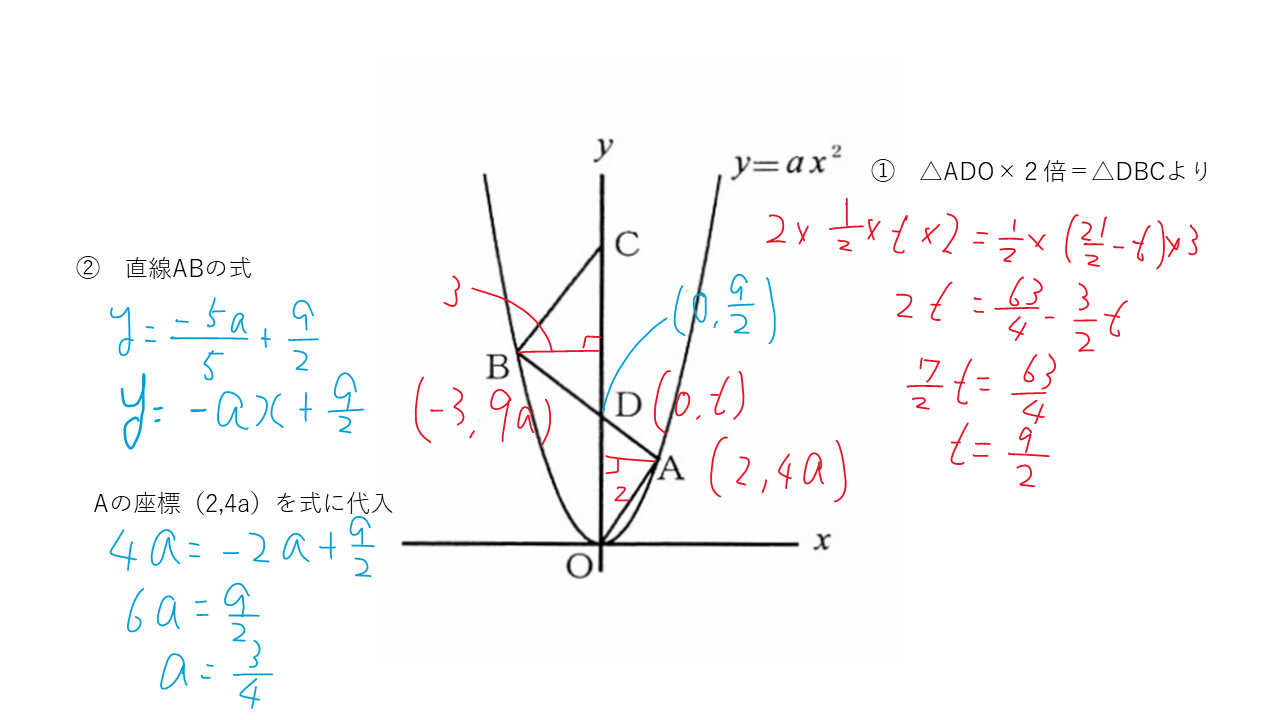
(2)関数と図形の問題(配点2点)
△CBDの面積が△DOAの面積の2倍という条件から、Dの座標をどう見つけるか。
そして、そこから直線ABの式を、aを使って求め、放物線との交点のAのx座標=2を代入してaを求める。
(3)兄、弟の移動をグラフにして解く問題(①が1点、②が2点)
①弟のグラフ(120m/分 5分で600m)を書き、6分後の点を読み取ればよい。
②兄のグラフを弟のグラフに重ね、交点の数を求める。
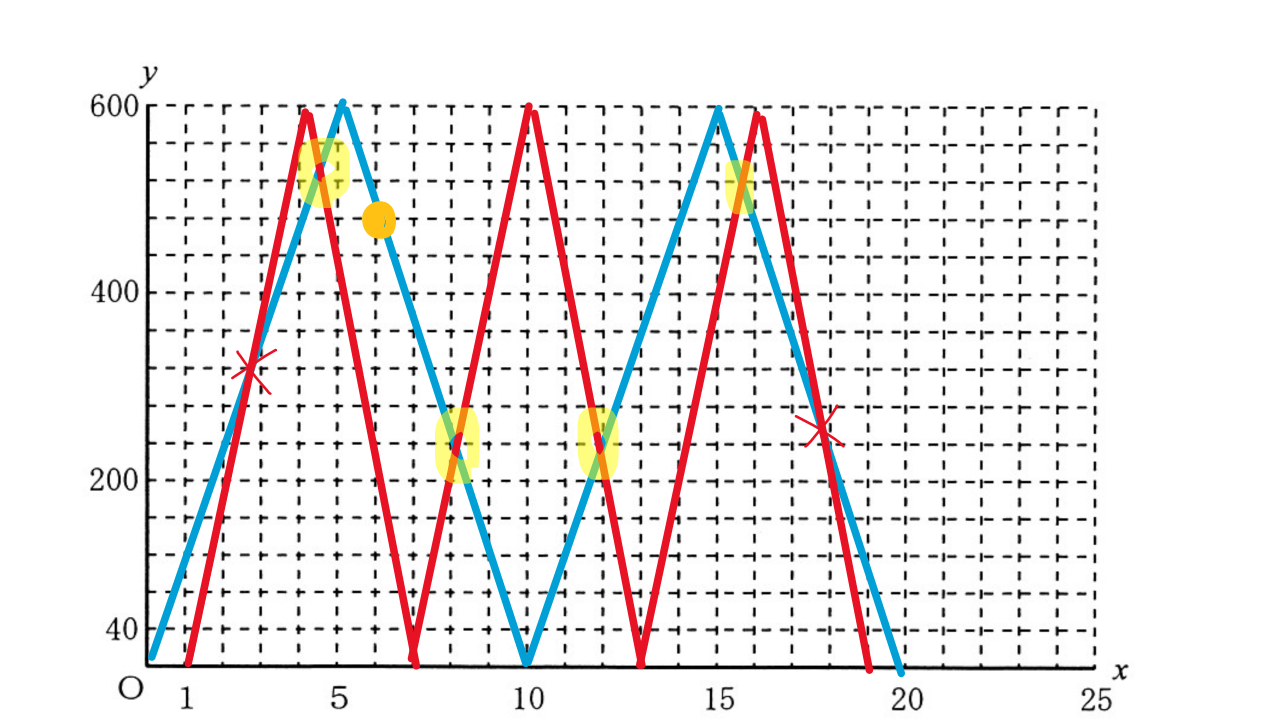
ただし、追い抜く場合を含めないとあるので、注意が必要!
3問ある2点問題のうち、(1)の場合の数の問題を落ち着いて数えられたかどうか。また、(3)のグラフの問題で、追い抜く場合を外すことができたか。
ここで、得点できたかどうかは、かなり大きいと思います。
大問3
図形問題
(1)
求角。
ACとFEの交点をGとすると、∠EGCは90°-21°=69°
EF//BCより、∠EGC=∠DCB=69°、∠FEB=∠EBC=21°
二等辺三角形の底辺は等しいので、∠ABC=69°
よって、∠ABD=∠ABC-∠EBC=69°-21°=48°
(2)図形・三平方の定理
①△EBCは直角三角形で、EC=2,BC=4、三平方の定理より、EB=2√5
FはEBの中点なので、EF=√5
②
ADとBEを延長した先の交点をPとする。
・△PGFと△PFAの相似からPGの長さを求めます
・△PDEと△PFGの相似からPHを求めます
・PF-PHでHFの長さを出し、EBとの比を求めます。
具体的には
△PAB∽△PDC(相似比は2:1)より
PA=8 PE=2√5 PF=3√5
△PGF∽△PFA
相似比からPGを求めると
PG:PF=PF:PA PG:3√5=3√5:8
PG=45/8
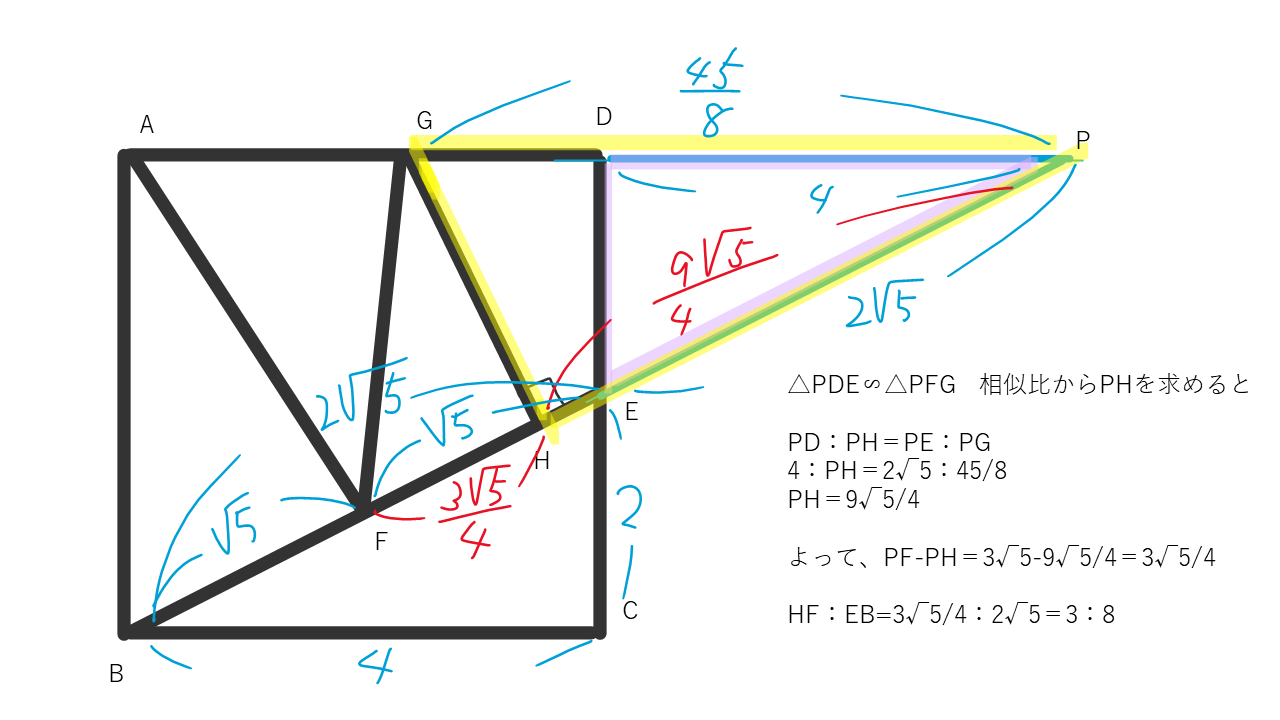
△PDE∽△PFG
相似比からPHを求めると
PD:PH=PE:PG
4:PH=2√5:45/8
PH=9√5/4
よって、
PF-PH=3√5-9√5/4=3√5/4
HF:EB=3√5/4:2√5=3:8
HF/EB=3/8倍

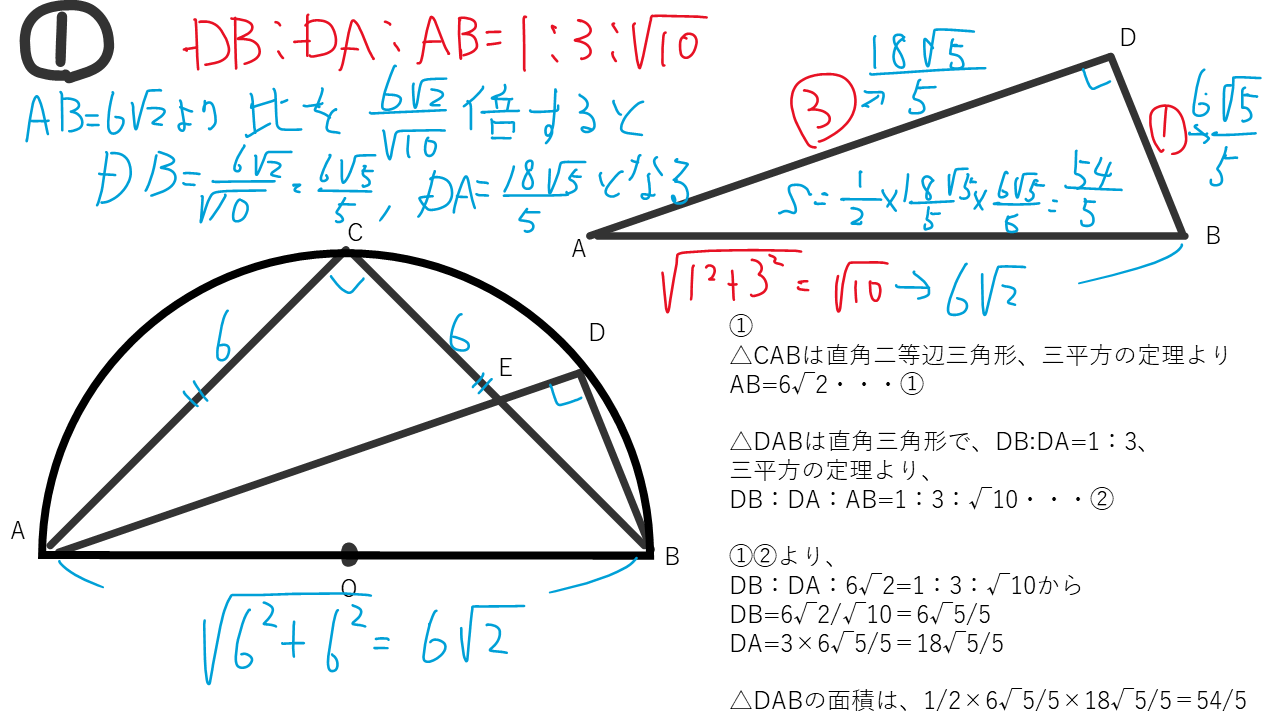
(3)①三平方の定理、相似など
△CABは直角二等辺三角形、三平方の定理よりAB=6√2・・・①
△DABは直角三角形で、DA:DB=1:3、三平方の定理より、
DB:DA:AB=1:3:√10・・・②
①②より、
DB:DA:6√2=1:3:√10から
DB=6√2/√10=6√5/5
DA=3×6√5/5=18√5/5
△DABの面積は、1/2×6√5/5×18√5/5=54/5
②三平方の定理、相似など
Eから線分ABに垂線をおろし、ABとの交点をFとします。
まずは、△ECAと△EDBの相似比からCE:EBの比を求めます。
次に、CE:EBの比から△BEFと△BCOの相似を求めEFを求めます。
最後に、EFを半径とする円を底面とし、高さがFAの円錐と、高さがFBの円錐の体積を求めます。
△ECA∽△EDB
相似比からECとEBの長さを求めます。
EC=xとおくと
CA:DB=EC:ED
6:6√5/5=x:ED
ED=√5/5x
EA=AD-ED=18√5/5-√5/5x=√5/5(18-x)
EB=CB-EC=6-x
EA:EB=CA:DB √5/5
(18-x):(6-x)=6:6√5/5
これを解いて、
x=3(EC=3)
また、EB=6-3=3 よって、
EC=EB=3となり、点Eは、CBの中点であることがわかる
EFは中点連結定理からEF=1/2 CO
COは半径なので、
CO=1/2×AB
=1/2×6√2
=3√2
EF=1/2×3√2
=3√2/2
EFを半径とする円を底面とし、高さがFAの円錐と、高さがFBの円錐の体積は
V=1/3×π×(3√2/2)^2×AF+1/3×π×(3√2/2)^2×FB
V=1/3×π×(3√2/2)^2×(AF+FB)
V=1/3×π×(3√2/2)^2×6√2
V=9√2π
全体を通して、大問2、大問3ともに全体が難化しており平均は、一昨年並の11~12点前後まで大きく下がると予想。
やはり、昨年が簡単すぎましたね。
来年以降も、数学は今年の難易度が基準になると思われます。
まずは、大問1を確実に満点取れるようにすることが一番大切ですね!








