2025年愛知の公立入試が無事終了、数学の詳しい解説はこちらへ!

日進市で、主に日進西中学校の生徒を中心に、生徒みずから主体性を持って学び、自分のペースで勉強できる、ICTを活用した自立学習による学びの場を提供している、セルモ日進西小学校前教室 塾長の西尾です。
本日無事、2025年の愛知県の公立高校一般入試の学力検査が終了しました。
2025年愛知の公立入試が無事終了、数学の詳しい解説はこちらへ!

友人の名学館小牧新町校の吉澤塾長が、個人で愛知県から入試当日の各教科の終了直後に問題、解答を入手し、即ブログにアップしてくれました!
今年も、吉澤塾長からの依頼もあって、数学の分析と解説を寄稿してみました。

昨年同様、最後の1問に苦しめられました~
とはいえ、大問1や、2がかなり優しくなった印象です。
平均点は、昨年より1~2点上がりそうだと予想しますね。
全体の所感
大問1 やや易
近年は、大問1にやや難しめの問題が入っていたが今年は、そこまで難易度の高い問題は無く、10点満点を取れた生徒も多いと思います。
大問2 やや易
(2)の問題が難しかったが、箱ひげ図もきちんと用語を抑えてあれば易しかったし、(3)も丁寧に二次関数のグラフと一次関数のグラフを書けば、計算しなくても答えは求まった。
大問3 例年並み
(1)求角や、(2)の相似は、例年並みの難易度でした。
√13を含む相似比の計算を自信を持って行えたか。
(3)の①は、三平方の定理で容易に求まるが、②は、かなり求めるのが難しい問題。
全体を通しては、昨年より、平均が1~2点上がると予想されます。
数学の解説
大問1
大問1は、昨年と同じく10問。
計算問題4問と、文章題、関数×2問、標本調査、確率、平面図形の小問6問の組み合わせとなっている。
難易度は、例年並みかやや易しくなっている感じ。
10問ある基本の1点問題で、いかにミスを少なくできたかが勝負の分かれ目かも。
大問2
(1)箱ひげ図の問題(2点問題)
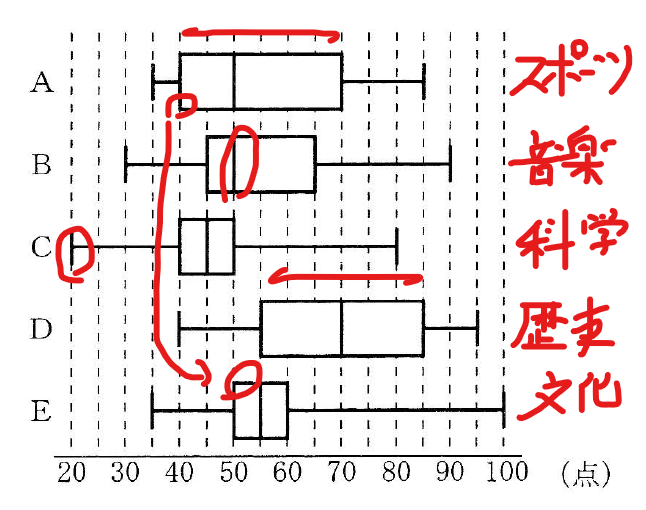
与えられた4つの条件からパズルを解くようにしていきます。
「箱ひげ図」は
左端 (最小値)
箱の左端 (第一四分位数)
箱の真ん中 (中央値)
箱の右端 (第三四分位数)
右端のヒゲ (最大値)
の位置を示します。
また四分位範囲は箱の幅となります。
①より、得点の最小値が一番小さい箱ひげ図は、CなのでC=「科学」
④「スポーツ」と「歴史」の四分位範囲が等しいより、AとDが「スポーツ」か「歴史」
③「文化」の第1四分位数は、「スポーツ」の第1四分位数より大きいと、④のAとDが「スポーツ」か「歴史」より、A=「スポーツ」、D=「歴史」
②「音楽」の「中央値」が 50 点より、B=「音楽」となる。
よって、、A=「スポーツ」B=「音楽」C=「科学」D=「歴史」E=「文化」となり答えに合致する記号は
ア「B:音楽,D:歴史」
となります
(2)関数と図形の融合問題(2点問題)
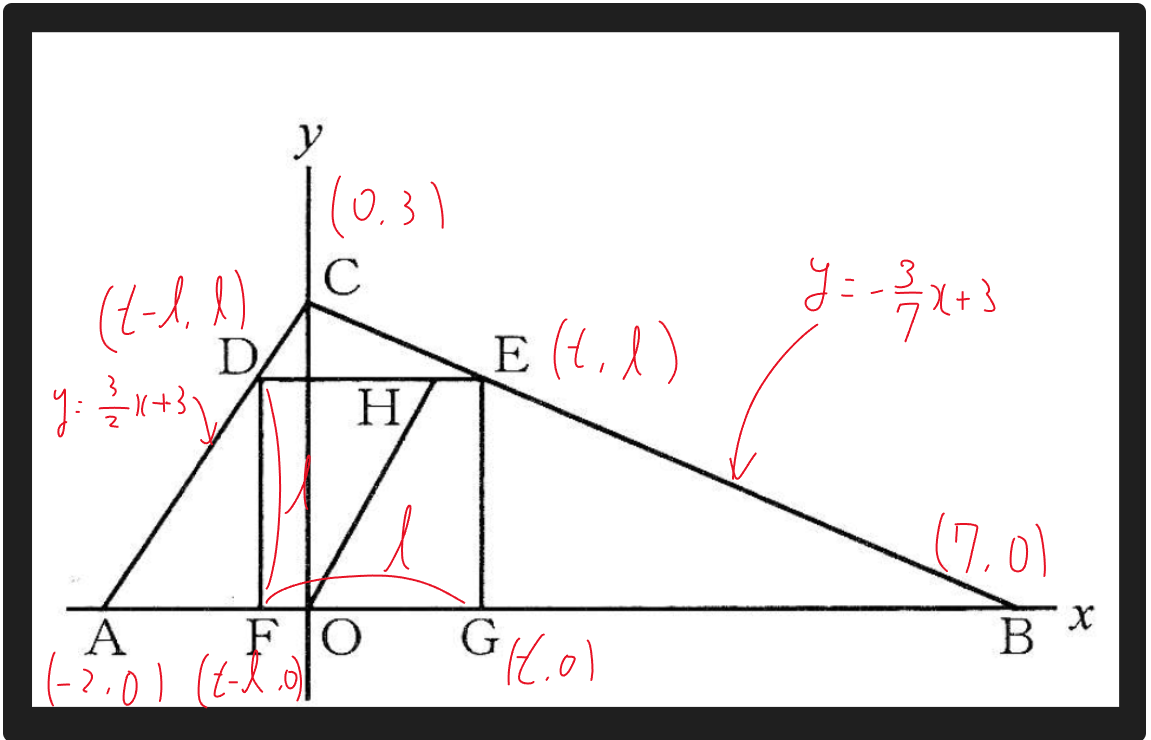
正方形の1辺の長さをℓ、Gのx座標をtと置くと、図のように各点を表すことができる。
ここで、Eのy座標はℓ=-3/7t+3…①、
また、Dのy座標は ℓ=3/2(t-ℓ)+3から、ℓ=3/5t+6/5…②
①と②より
-3/7t+3=3/5t+6/5
t=7/4
①に代入して、
ℓ=9/4
面積を等しくするためには、OF=EHとなればいいので、
OF=ℓ-t=9/4-7/4=1/2
よってHのx座標は、7/4-1/2=5/4
答えはエのx=5/4
(3)長方形の周りをまわる点P,Q,Rが作る三角形の面積を表すグラフの問題。(1点&2点問題)
①1点問題
△APQの面積をyとすると
y=1/2*x*2x=x^2となる
x=3のyの値は、y=9
答えはイのy=9
②(2点問題)
△APQと、△ABRをグラフにすると図の通りになる。
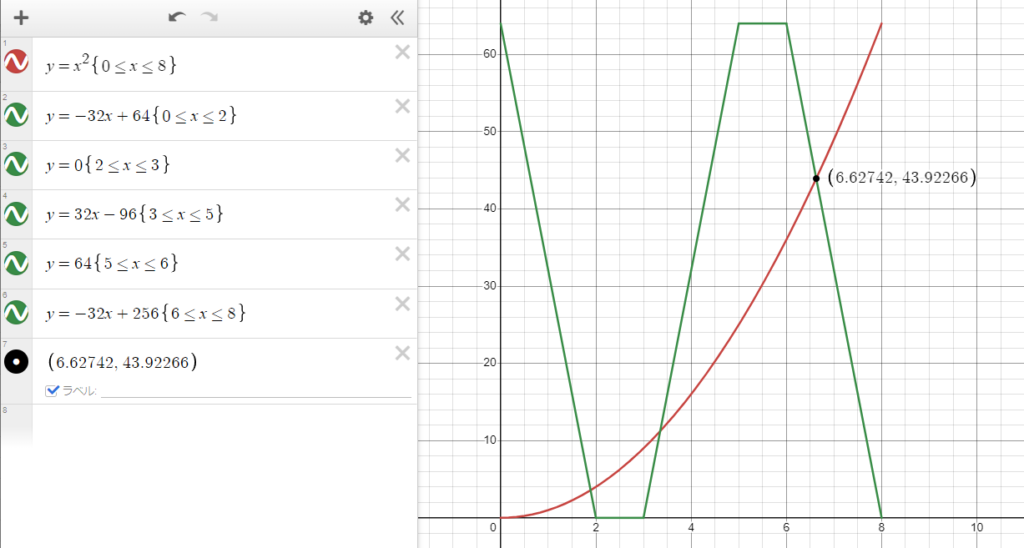
3回目の交点はグラフより、
オ 6秒後から7秒後までの間。
(別解)
y=-32x+256と
y=x^2の交点を式から求めると
x^2+32x-256=0
x=-16+16√2
≒6.72
オ 6秒後から7秒後までの間。
3問ある2点問題のうち、(1)箱ひげ図を落ち着いて答えられたかどうか。また、(3)のグラフの問題で放物線を正確に描けたか。
ここで、得点できたかどうかは、かなり大きいと思います。
大問3
図形問題
(1)
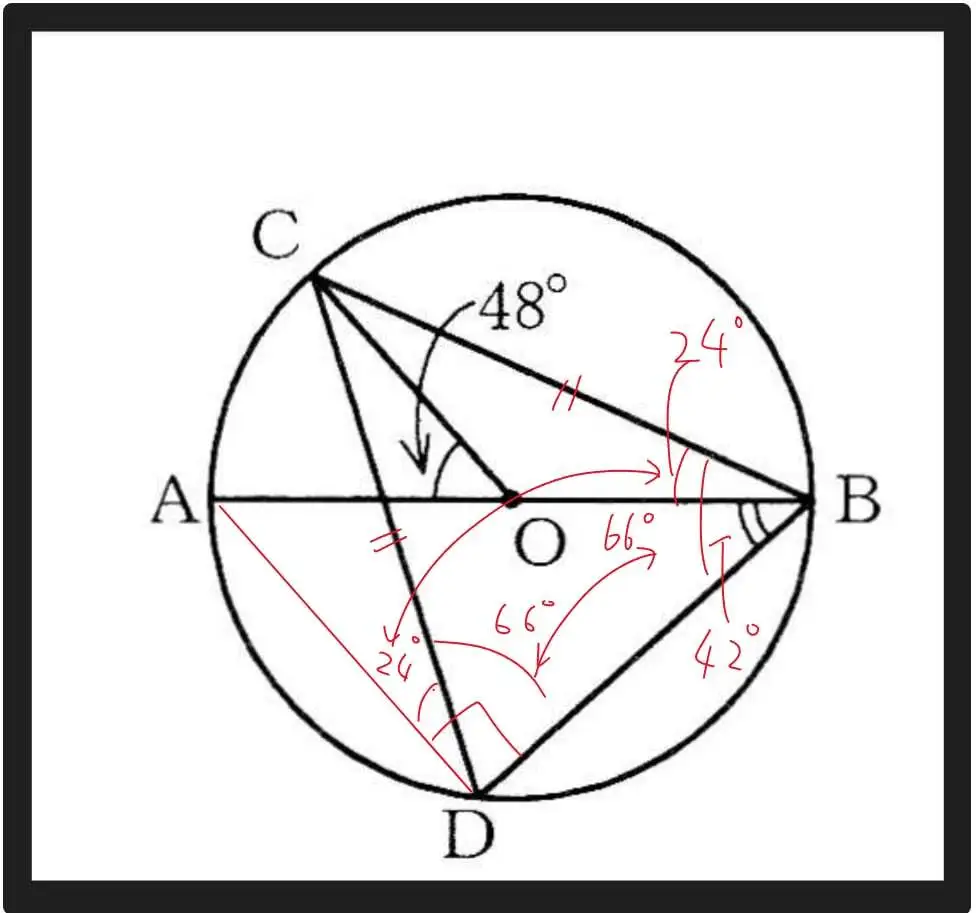
求角。
弧CAの中心角48°より、円周角24°(∠CBA=∠CDA=24°)
ABが直径なので、∠ADB=90° ∠CDB=90-24=66°
CD=CBの二等辺三角形なので、∠CBD=66°
∠ABD=66-24=42°
答え 42度
(2)図形・相似・三平方の定理
①
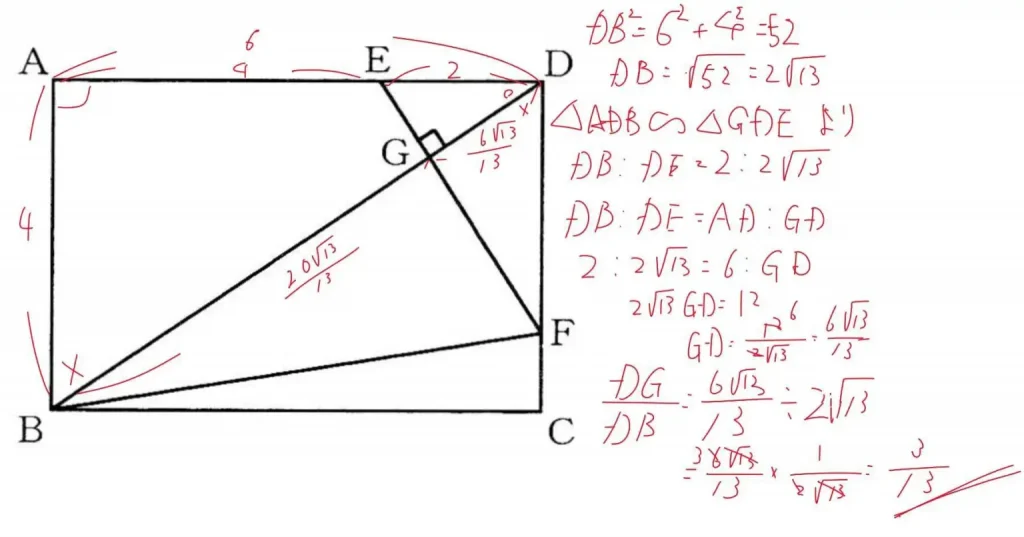
②
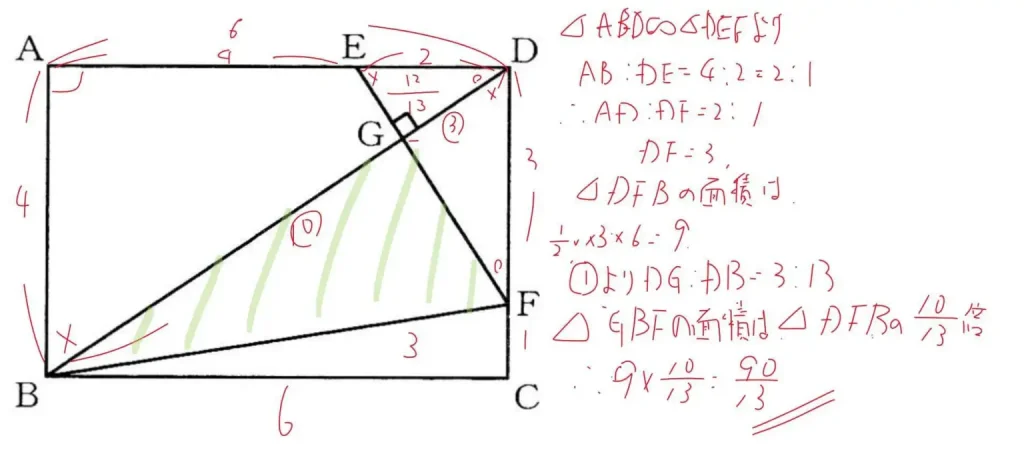
(3)立体図形・三平方の定理・体積比
①底面の1辺6cmの正方形の対角線BDの長さは三平方の定理より6√2
頂点Oから底面ABCDの中心Iへ推薦OIを下したとき、DI=BI=3√2
三平方の定理より、OI=3√14
△OBDの面積=1/2*6√2*3√14=18√7
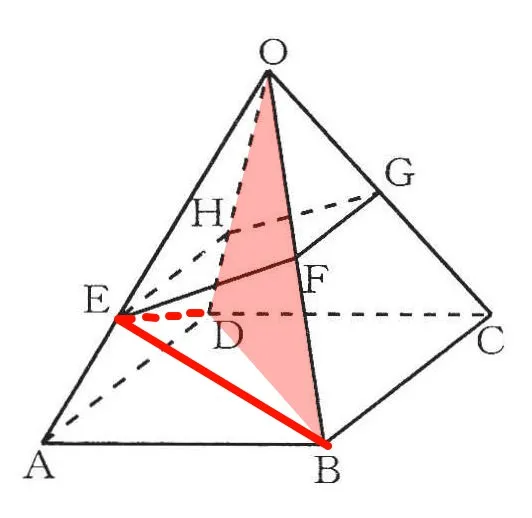
②
三角形OBDを底面として、三角錐A-OBDを考える。
その体積に対して三角錐E-OBDは高さが2/3倍になっている。
なので、A-OBDの体積の2/3倍
よって、E-ODBの体積=2/3*A-OBD
同様に、今度はOEDを底面にして、高さが、OF:OBの比で1/2
F-OED=1/2*E-ODB=1/2*2/3*A-OBD
同様にOEFを底面にし、D-OEFで考えると、OH:ODの比で2/3
H-OEF=2/3D-OEF=2/3*1/2*2/3*A-OBD
三角錐A-OBDの体積は、底面が△ABC なので,正方形の半分で18
よって、O-ABCDの体積=1/3*18*3√14=18√14
H-OEF=2/3*1/2*2/3*18√14
=4√14
同様に、反対のC-OBDで同じことをやると
G-OFH=1/2*1/2*2/3*C-OBD==3√14
O-EFGH=H-OEF + G-OFH
=4√14+3√14=7√14
全体を通して、大問2、大問3ともに昨年並みか、やや易化しており、平均は、昨年から1~2点上昇し13点前後まで上がると予想。
来年以降も、数学は今年の難易度が基準になると思われます。
まずは、大問1を確実に満点取れるようにすることが一番大切ですね!








